One can treat electrical and thermal conduction and the thermoelectric effects in semiconductors in a unified approach using the concept of “differential conductivity” (i.e. conductivity of electrons with a given energy inside the solid). The traditional derivation based on the Boltzmann transport equation and relaxation time approximation is calculation intensive and it is not appropriate for undergraduate education. It is also difficult to gain insight about the underlying physics. Here we created a user-friendly interface for the Boltzmann transport equation. The key functions such as density-of-states, Fermi-Dirac distribution function and differential conductivity are plotted versus electron energy. Electron mobility, electrical conductivity and Seebeck coefficient are accurately calculated based on the transport model described below. One can change the material properties (such as electron effective mass and mean-free-time between collisions) or the ambient temperature and see how these graphs are modified and what is the effect in the overall conductivity and Seebeck coefficient.

Detail of the Applets:

Input parameters:
• Electron effective mass (m*)
Electrons inside a solid can have a different mass than an isolated electron. This takes into account interactions with atoms inside a crystal and it represents the inertial resistance of an electron inside a crystal against an acceleration imposed by an external force such as the applied electric field.
• Mean-free-time between collisions (t)
This is the average time it takes to scatter a conduction electron.
• Temperature (T)
This is the ambient temperature.

Functions plotted:
• Density-of-States (n(E))
This is the number of electron states per unit energy per unit volume. n(E)dE is thus the number of states in the energy range E to E+dE per unit volume.
• Fermi-Dirac distribution function (f(E))
Fermi-Dirac statistics determines the probability of occupancy of a state at an energy level E by an electron. It takes into account that when we are considering a collection of electrons, they must obey the Pauli Exclusion Principle. The Fermi-Dirac function quantifies this probability via f(E) = 1/[(1+exp(E - E_F))/kT] where E_Fis the Fermi energy, k is the Boltzmann constant and T is the temperature (Kelvins).
• Differential conductivity (s(E))
This represents how electrons with a given energy inside the solid contribute to overall electrical conductivity of the material.

Material properties calculated:
• Electron Mobility (m)
This describes how easily each electron moves in the material under an electric field. This is the drift velocity per unit applied electric field. If ? is the drift mobility then the defining equation is vd = mE where vd is the drift velocity and E is the electric field. The drift mobility is related to the mean free time by m = et/m.
• Electrical Conductivity (s)
This is a property of a material that quantifies how much current flows inside the material along an applied electric field. It is the inverse of electrical resistivity, r. s is the rate of charge flow through a unit area per unit voltage gradient; J = sE, where J is the current density and E is the electric field. If electron concentration is n, and the electron drift mobility is m, the conductivity is given by s = enm, where e is the electronic charge.
• Seebeck Coefficient (S)
This is related to the development of a built-in potential difference across a material as a result of a temperature gradient. If dV is the built-in potential across the materials when there is a temperature difference dT, then the Seebeck coefficient S is defined by S = dV/dT. The principle of the thermocouple is based on the Seebeck effect.

The current density and heat flux carried by electrons can be expressed as [1]

(1)

(2)

where q is the unit charge of each carrier, E_f the Fermi energy, v the carrier velocity, and the integration is over all the possible wavevectors k of all the charges. The carrier probability distribution function, f(r,k) is governed by the Boltzmann equation. Considering transport processes occurring much slower than the relaxation process and employing the relaxation time approximation, the Boltzmann equation can be expressed as:

(3)

where e the electric field, t(k) the momentum-dependent relaxation time, the Planck constant divided by 2p, and f_eq the equilibrium distribution function. For electrons and holes,

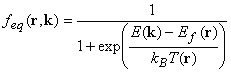(4)

where k_B is the Boltzmann constant and T the local temperature. Under the further assumption that the local deviation from equilibrium is small, the Boltzmann equation can be linearized and its solution expressed as

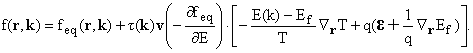(5)

Substituting the above expression in Eqs. (1) and (2) leads to the

(6)

(7)

where F is the electrochemical potential ( ). The transport coefficients L_n are defined by the following integral

(8)

From the expressions for J and J_Q, various material parameters such as the electrical conductivity, thermal conductivity due to electrons, and the Seebeck coefficient can be calculated. For simplicity we assume that both the current flow and the temperature gradient are in the x-direction:

(9)

(10)

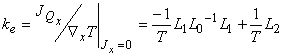(11)

Rewriting the expressions for electrical conductivity and the thermopower in the form of integrals over the electron energy we get:

(12)

(13)

where we introduced the "differential" conductivity,

(14)

where n(E) is the density of states. s (E) is a measure of the contribution of electrons with energy E to the total conductivity. The Fermi "window" factor (- _feq/ E) is a bell-shape function centered at E=E_f, having a width of ˜k_BT. At a finite temperature only electrons near the Fermi surface contribute to the conduction process. In this picture, the thermopower is the "average" energy transported by the charge carriers. In order to achieve the best thermoelectric properties, s (E), within the Fermi window, should be as big as possible, and at the same time, as asymmetric as possible with respect to the Fermi energy.

Figures below show a graphical representation of the differential conductivity. This quantifies how electrons with a given energy contribute to the conduction process. We have developed a user-friendly interface for the transport equations, creating animations of electron transport in semiconductors. Students will not have to go through the detailed mathematical derivation shown above to get an intuitive understanding of what is happening inside semiconductors. Students can see how changing the effective mass of electrons modifies their average transport energy, and how this affects the amount of cooling or heating at the interface between two materials.

Note: It is interesting to note that the thermal conductivity due to lattice vibration is also often modeled from the Boltzmann equation under the relaxation time approximation,

(15)

where C is the specific heat of phonons at frequency w, v_p the phonon group velocity, and ? the phonon mean free path. The graphical representation shown below can be generalized to explain heat transport in various materials as well.

[1] Aschroft, N.W. and Mermin, N.D., 1976, Solid State Physics, Saunders College Publishing, Fort Worth.